Moments of Inertia
In physics and applied mathematics, the mass moment of inertia, usually denoted by `I`, measures the extent to which an object resists rotational acceleration about a particular axis, and is the rotational analogue to mass. Mass moments of inertia have units of dimension ML2([mass]*[length]2). It should not be confused with the second moment of area, which is used in bending calculations. The mass moment of inertia is often known as rotational inertia, and sometimes as the angular mass.
For simple objects with geometric symmetry, one can often determine the inertia in an exact closed-form expression. Typically this occurs when the mass density is constant, but in some cases the density can vary throughout the object as well. In general, it may not be straightforward to symbolically express the moment of inertia of shapes with more complicated mass distributions and lacking symmetry. When calculating moments of inertia, it is useful to remember that it is an additive function and exploit the parallel axis and perendicular axis therorms.
| Description | Figure | Moment(s) of Inertia |
| Point Mass | ||
| Rod rotating about center | 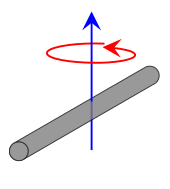 |
|
| Rod rotating about end | 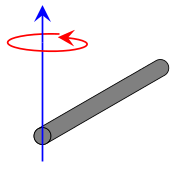 |
|
| Hoop | 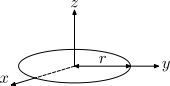 |
|
| Solid Disk | 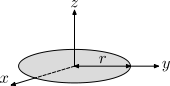 |
|
| Cylindrical Shell | 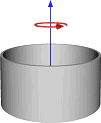 |
|
| Solid Cylinder | 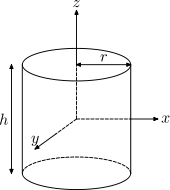 |
|
| Thick-walled Cylinder | 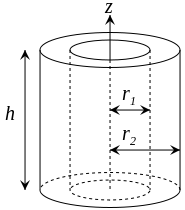 |
Using Density: |
| Tetrahedron | 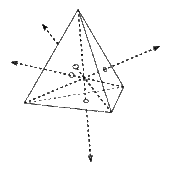 |
|
| Octahedron | 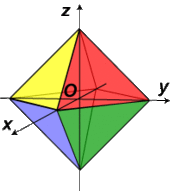 |
|
| Dodecahedron | ||
| Icosahedron | ||
| Hollow Sphere | 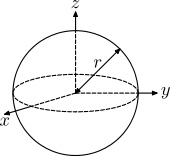 |
|
| Solid Sphere | 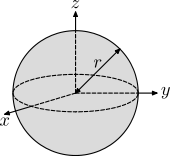 |
|
| Sphere Shell | 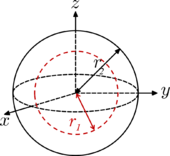 |
|
| Right circular cone | 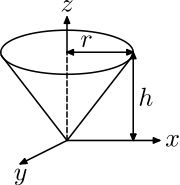 |
|
| Torus | 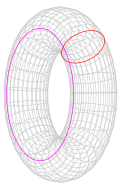 |
About axis: About diameter: |
| Ellipsoid | 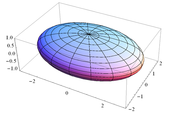 |
|
| Rectangular Plate rotating around end | 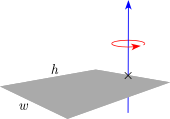 |
|
| Rectangular Plate rotating around center | 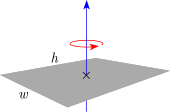 |
|
| Solid Cuboid | 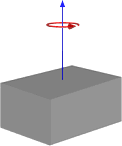 |
References
Wikipedia (https://en.wikipedia.org/wiki/List_of_moments_of_inertia)